Question

Using a scale diagram, calculate the resultant force acting on a sailing boat when an easterly wind provides 2, point, 50, k, N,2.50kN of force, the tide provides 1, point, 20, k, N,1.20kN of force from the direction 30, point, 0, degrees,30.0 ∘ more northerly than the wind. Give your answer to 2 significant figures. Remember that 'an easterly wind' means a wind coming from the East

Answer 1

F = 3.6 kN, direction is 9.6º to the North - East

Step-by-step explanation:

The force is a vector, so one method to find the solution is to work with the components of the vector as scalars and then construct the resulting vector.

Let's use trigonometry to find the component of the forces, let's use a reference frame where the x-axis coincides with the East and the y-axis coincides with the North.

Wind

X axis

F₁ = 2.50 kN

Tide

cos 30 = F₂ₓ / F₂

sin 30 = F_{2y} / F₂

F₂ₓ = F₂ cos 30

F_{2y} = F₂ sin 30

F₂ₓ = 1.20cos 30 = 1.039 kN

F_{2y} = 1.20 sin 30 = 0.600 kN

the resultant force is

X axis

Fₓ = F₁ₓ + F₂ₓ

Fₓ = 2.50 +1.039

Fₓ = 3,539 kN

F_y = F_{2y}

F_y = 0.600

to find the vector we use the Pythagorean theorem

F =
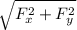
`√(F_x^2 +F_y^2)`

F =
`√( 3.539^2 + 0.600^2 )`

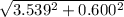
F = 3,589 kN

the address is

tan θ = F_y / Fₓ

θ = tan⁻¹
`(F_y)/(F_x)`

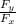
θ = tan⁻¹
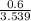`(0.6)/(3.539)`0.6 / 3.539

θ = 9.6º

the resultant force to two significant figures is

F = 3.6 kN

the direction is 9.6º to the North - East