Question

Classes. frequency

0-20 2
20-40. 2
40-60. 3
60-80 12
80-100 18
100-120 5
120-140. 2

Find mean, median and mode​

Answer 1

The mean is 79.
`\overline {54}`

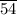
The median is 80 - 100

The mode is 80 - 100

Step-by-step explanation:

The given table is presented as follows;

`\begin{array}{lcrc}Classes&Mid \ point &Frequency &Frequency * Mid \ point\\0 - 20&10& 2&20\\20-40&30&2&60\\40-60&50&3&150\\60-80&70&12&840\\80-100&90&18&1620\\100-120&110&5&550\\120-140&130&2&260\end{array}`

The mean of a class of values,
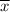`\overline x` = ∑(Frequency × Midpoint)/∑(Frequency)

Therefore, we get;

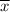`\overline x` = (20+60+150+840+1620+550+260)/(2+2+3+12+18+5+2) = 79.
`\overline {54}`

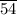
The mean,
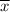`\overline x` =79.
`\overline {54}`

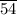
The median class = The middle value lass = The class at the 22 nd value = 80 - 100

The median = 80 - 100

The modal class = The class with the highest frequency = 80 - 100

The mode = 80 - 100