Question

If charge on only one object is tripled, determine the new force between them:

Answer 1

+3·F

Step-by-step explanation:

The number of objects in the given system = 2 objects

The charge on each object are; q₁ = -Q, q₂ = -Q

The force acting between the objects = +F

The distance between the objects = 2·d

The formula for the force acting between two charged particles is given as follows;

`F=K * (q_(1) * q_(2))/(r^(2))`

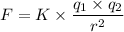
Therefore, we get;

`F=K * (-Q * -Q)/((2\cdot d)^(2)) = K * (Q^2)/(4 \cdot d^2)`

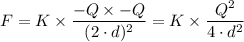
By tripling the charge, q₁, on the first object, we get;

q₂ = 3 × (-Q)

`F_2=K * (-3 \cdot Q * -Q)/((2\cdot d)^(2)) = K * (3 \cdot Q^2)/(4 \cdot d^2) = 3 * +F = +3\cdot F`

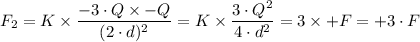
Therefore, the new force between them, F₂ = +3·F