Question

If f(x) =4x2 - 8x - 20 and g(x) = 2x + a, find the value of a so that the y-intercept of the graph of the composite function (fog)(x) is (0, 25).

Answer 1

The possible values are a = -2.5 or a = 4.5.

Explanation:

Composite function:

The composite function of f(x) and g(x) is given by:

`(f \circ g)(x) = f(g(x))`

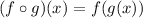
In this case:

`f(x) = 4x^2 - 8x - 20`

`g(x) = 2x + a`

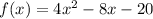
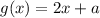
So

`(f \circ g)(x) = f(g(x)) = f(2x + a) = 4(2x + a)^2 - 8(2x + a) - 20 = 4(4x^2 + 4ax + a^2) - 16x - 8a - 20 = 16x^2 + 16ax + 4a^2 - 16x - 8a - 20 = 16x^2 +(16a-16)x + 4a^2 - 8a - 20`

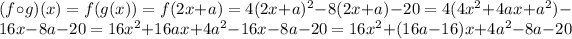
Value of a so that the y-intercept of the graph of the composite function (fog)(x) is (0, 25).

This means that when
`x = 0, f(g(x)) = 25`. So

`4a^2 - 8a - 20 = 25`

`4a^2 - 8a - 45 = 0`

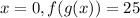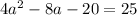
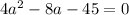
Solving a quadratic equation, by Bhaskara:

`\Delta = (-8)^2 - 4(4)(-45) = 784`

`x_(1) = (-(-8) + √(784))/(2*(4)) = (36)/(8) = 4.5`

`x_(2) = (-(-8) - √(784))/(2*(4)) = -(20)/(8) = -2.5`

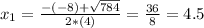
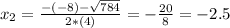
The possible values are a = -2.5 or a = 4.5.