Answer:
The other angle is 75⁰
Step-by-step explanation:
Given;
velocity of the projectile, v = 10 m/s
range of the projectile, R = 5.1 m
angle of projection, 15⁰
The range of a projectile is given as;
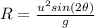
To find another angle of projection to give the same range;

Check:
sin(2θ) = sin(2 x 75) = sin(150) = 0.5
sin(2θ) = sin(2 x 15) = sin(30) = 0.5