Answer:
(a)
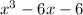
(b) Proved
Explanation:
Given
![r = $\sqrt[3]{2} + \sqrt[3]{4}$](https://img.qammunity.org/2022/formulas/mathematics/high-school/ywbxziya7jn32w43ss8rta7hl7zxghpou9.png) --- the root
--- the root
Solving (a): The polynomial
A cubic function is represented as:
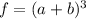
Expand
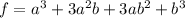
Rewrite as:
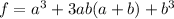
The root is represented as:
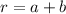
By comparison:
![a = $\sqrt[3]{2}](https://img.qammunity.org/2022/formulas/mathematics/high-school/mzr3gcz1w200swmjl2cli5cq5gjqmbwhbm.png)
![b = \sqrt[3]{4}$](https://img.qammunity.org/2022/formulas/mathematics/high-school/lh16d0iezum4q6n3166ocmuzy0zy4h5ryt.png)
So, we have:
![f = ($\sqrt[3]{2})^3 + 3*$\sqrt[3]{2}*\sqrt[3]{4}$*($\sqrt[3]{2} + \sqrt[3]{4}$) + (\sqrt[3]{4}$)^3](https://img.qammunity.org/2022/formulas/mathematics/high-school/csb2rziixlq2ih3hrn3wjabsc2dxiw0u62.png)
Expand
![f = 2 + 3*$\sqrt[3]{2*4}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/2022/formulas/mathematics/high-school/fmuf51g7qwlz19fsfmaxnpk7x2gghkg9h0.png)
![f = 2 + 3*$\sqrt[3]{8}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/2022/formulas/mathematics/high-school/6t2wquhyy7rbklkt7zw6c8mjkp1bjggb4m.png)
![f = 2 + 3*2*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/2022/formulas/mathematics/high-school/gf3rgy9lnvx6ulfsy3833ozwml3bk46pjo.png)
![f = 2 + 6($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/2022/formulas/mathematics/high-school/m5t8nlidk8szc9p5fti9h3o0368xwachhd.png)
Evaluate like terms
![f = 6 + 6($\sqrt[3]{2} + \sqrt[3]{4}$)](https://img.qammunity.org/2022/formulas/mathematics/high-school/hgxgliw4650fyu9pxic7wetwx612wff111.png)
Recall that:
![r = $\sqrt[3]{2} + \sqrt[3]{4}$](https://img.qammunity.org/2022/formulas/mathematics/high-school/ywbxziya7jn32w43ss8rta7hl7zxghpou9.png)
So, we have:
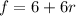
Equate to 0
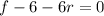
Rewrite as:
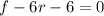
Express as a cubic function
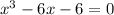
Hence, the cubic polynomial is:
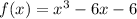
Solving (b): Prove that r is irrational
The constant term of
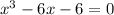 is -6
is -6
The divisors of -6 are: -6,-3,-2,-1,1,2,3,6
Calculate f(x) for each of the above values to calculate the remainder when f(x) is divided by any of the above values
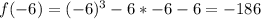
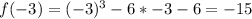
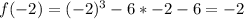
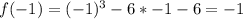
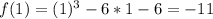
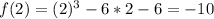
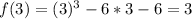
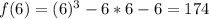
For r to be rational;
The divisors of -6 must divide f(x) without remainder
i.e. Any of the above values must equal 0
Since none equals 0, then r is irrational