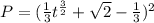Question

Find the solution of the differential equation that satisfies the given initial condition. (dP)/(dt)

Answer 1

`P = ((1)/(3)t^(3)/(2) + \sqrt 2 - (1)/(3))^2`

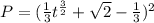
Explanation:

Given

`(dP)/(dt) = \sqrt{Pt`

`P(1) = 2`

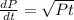
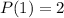
Required

The solution

We have:

`(dP)/(dt) = \sqrt{Pt`

`(dP)/(dt) = (Pt)^(1)/(2)`

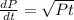
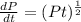
Split

`(dP)/(dt) = P^(1)/(2) * t^(1)/(2)`

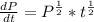
Divide both sides by
`P^(1)/(2)`

`(dP)/( P^(1)/(2)*dt) = t^(1)/(2)`

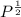
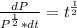
Multiply both sides by dt

`(dP)/( P^(1)/(2)) = t^(1)/(2) \cdot dt`

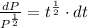
Integrate

`\int (dP)/( P^(1)/(2)) = \int t^(1)/(2) \cdot dt`

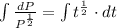
Rewrite as:

`\int dP \cdot P^(-1)/(2) = \int t^(1)/(2) \cdot dt`

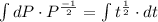
Integrate the left hand side

`\frac{P^{(-1)/(2)+1}}{(-1)/(2)+1} = \int t^(1)/(2) \cdot dt`

`\frac{P^{(-1)/(2)+1}}{(1)/(2)} = \int t^(1)/(2) \cdot dt`

`2P^{(1)/(2)} = \int t^(1)/(2) \cdot dt`

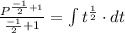
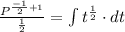
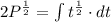
Integrate the right hand side

`2P^{(1)/(2)} = \frac{t^{(1)/(2) +1 }}{(1)/(2) +1 } + c`

`2P^{(1)/(2)} = \frac{t^{(3)/(2)}}{(3)/(2) } + c`

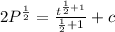
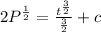
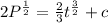`2P^{(1)/(2)} = (2)/(3)t^(3)/(2) + c` ---- (1)

To solve for c, we first make c the subject

`c = 2P^{(1)/(2)} - (2)/(3)t^(3)/(2)`

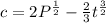
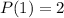`P(1) = 2` means

`t = 1; P =2`

So:

`c = 2*2^{(1)/(2)} - (2)/(3)*1^(3)/(2)`

`c = 2*2^{(1)/(2)} - (2)/(3)*1`

`c = 2\sqrt 2 - (2)/(3)`

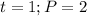
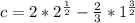
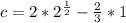
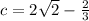
So, we have:

`2P^{(1)/(2)} = (2)/(3)t^(3)/(2) + c`

`2P^{(1)/(2)} = (2)/(3)t^(3)/(2) + 2\sqrt 2 - (2)/(3)`

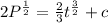
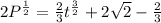
Divide through by 2

`P^{(1)/(2)} = (1)/(3)t^(3)/(2) + \sqrt 2 - (1)/(3)`

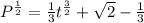
Square both sides

`P = ((1)/(3)t^(3)/(2) + \sqrt 2 - (1)/(3))^2`