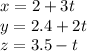Question

Find a vector equation and parametric equations for the line The line through the point (2, 2.4, 3.5) and parallel to the vector 3i 1 2j 2 k

Answer 1

The vector equation

`r = (2 + 3t)i+ (2.4 + 2t)j+ (3.5 - t)k`

The parametric equation

`x = 2 + 3t\\y = 2.4 + 2t\\z = 3.5-t`

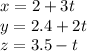
Explanation:

Given

`Point = (2,2.4,3.5)`

`Vector = 3i + 2j - k`

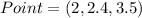
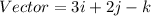
Required

The vector equation

First, we calculate the position vector of the point.

This is represented as:

`r_0 = 2i + 2.4j + 3.5k`

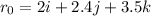
The vector equation is then calculated as:

`r = r_o + t * Vector`

`r = 2i + 2.4j + 3.5k + t * (3i + 2j - k)`

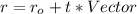
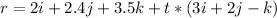
Open bracket

`r = 2i + 2.4j + 3.5k + 3ti + 2tj - tk`

Collect like terms

`r = 2i + 3ti+ 2.4j + 2tj+ 3.5k - tk`

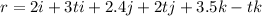
Factorize

`r = (2 + 3t)i+ (2.4 + 2t)j+ (3.5 - t)k`

The parametric equation is represented as:

`x = x_0 + at\\y = y_0 + bt\\z = z_0 + ct`

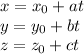
Where

`r = (x_0 + at)i +(y_0 + bt)j+(z_0 + ct)k`

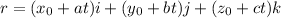
By comparison:

`x = 2 + 3t\\y = 2.4 + 2t\\z = 3.5-t`