Question

rom each corner of a square piece of sheet metal 18 centimeters on a side,we remove a small square and turn up the edges to form an open box. Whatis the largest volume this box could have

Answer 1

The volume is maximum when the height is 3 cm.

Explanation:

let the side of the removed potion is x.

length of the box = 18 - 2 x

width of the box = 18 - 2 x

height = x

Volume of box

V = Length x width x height

`V = (18 - 2 x)^2 * x\\\\V = x(324 + 4x^2 - 72 x)\\\\V = 4 x^3 - 72 x^2 + 324 x \\\\(dV)/(dx) = 12 x^2 - 144 x + 324 \\\\So,\\\\ (dV)/(dx) =0\\\\x^2 - 12 x + 27 = 0 \\\\x^2 -9 x - 3 x + 27 =0\\\\x (x - 9) - 3 (x -9) = 0\\\\x = 3, 9`

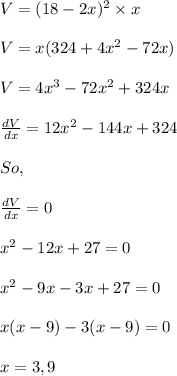
Now

`(d^2V)/(dx^2)=24 x - 144 \\\\Put x = 3 \\\\(d^2V)/(dx^2)=24* 3 - 144 = - 72\\\\Put x = 9\\\\(d^2V)/(dx^2)=24* 9 - 144 = 72\\`

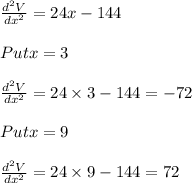
So, the volume is maximum when x = 3 .