Question

The mass per unit length of the rope is 0.0500 kg/m. Find the tension. Express your answer in newtons.

Answer 1

Complete question:

A transverse wave on a rope is given by
`y \ (x, \ t) = (0.75 \ cm) \ cos \ \pi[(0.400 \ cm^(-1)) x + (250 \ s^(-1))t]`. The mass per unit length of the rope is 0.0500 kg/m. Find the tension. Express your answer in newtons.

Answer:

The tension on the rope is 1.95 N

Step-by-step explanation:

The general equation of a progressive wave is given as;

`y \ (x,t) = A \ cos(kx \ + \omega t)`

Compare the given equation with the general equation of wave, the following parameters will be deduced.

A = 0.75 cm

k = 0.400π cm⁻¹

ω = 250π s⁻¹

The frequency of the wave is calculated as;

ω = 2πf

2πf = 250π

2f = 250

f = 250/2

f = 125 Hz

The wavelength of the wave is calculated as;

`\lambda = (2\pi)/(k) \\\\\lambda = (2\pi )/(0.4 \pi) = 5 \ cm = 0.05 \ m`

The velocity of the wave is calculated as;

v = fλ

v = 125 x 0.05

v = 6.25 m/s

The tension on the rope is calculated as;

`v = \sqrt{(T)/(\mu)} \\\\where;\\\\T \ is \ the \ tension \ of \ the \ rope\\\\\mu \ is \ the \ mass \ per \ unit \ length = 0.05 \ kg/m\\\\v^2 = (T)/(\mu) \\\\T = v^2 \mu\\\\T = (6.25)^2* (0.05)\\\\T = 1.95 \ N`

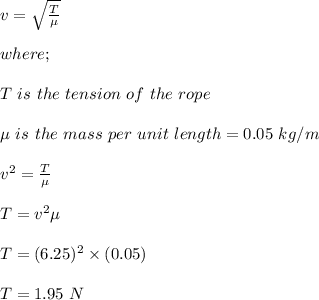
Therefore, the tension on the rope is 1.95 N