Is it possible to have a relation on the set {a, b, c} that is both symmetric and transitive but not reflexive

Question

asked May 13, 2022 172k views

1 Answer

Nagesh Salunke · Answer 1 · 2022-05-19T17:05:04+0000

Answer:

Yes, it is possible to have a relation on the set {a, b, c} that is both symmetric and transitive but not reflexive

Explanation:

Let

Set A={a,b,c}

Now, define a relation R on set A is given by

R={(a,a),(a,b),(b,a),(b,b)}

For reflexive

A relation is called reflexive if (a,a)
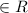$\in R$ for every element a
$\in A$

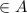
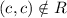
$(c,c)\\otin R$

Therefore, the relation R is not reflexive.

For symmetric

If
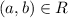$(a,b)\in R$ then
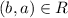
$(b,a)\in R$

We have

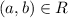$(a,b)\in R$ and
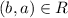
$(b,a)\in R$

Hence, R is symmetric.

For transitive

If (a,b)
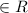$\in R$ and (b,c)
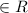$\in R$ then (a,c)
$\in R$

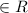
Here,

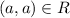$(a,a)\in R$ and
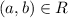
$(a,b)\in R$

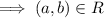
$\implies (a,b)\in R$

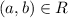$(a,b)\in R$ and
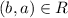
$(b,a)\in R$

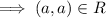
$\implies (a,a)\in R$

Therefore, R is transitive.

Yes, it is possible to have a relation on the set {a, b, c} that is both symmetric and transitive but not reflexive.