Question

HELP HELP HELPPPP PLEASEEE

Directions: Determine if segments AB and CD are parallel, perpendicular, or neither.
AB formed by (-2, 13) and (0, 3)
CD formed by (-5, 0) and (10, 3)

Answer 1

Given:

AB formed by (-2,13) and (0,3).

CD formed by (-5,0) and (10,3).

To find:

Whether the segments AB and CD are parallel, perpendicular, or neither.

Solution:

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

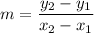
AB formed by (-2,13) and (0,3). So, the slope of AB is:

`m_1=(3-13)/(0-(-2))`

`m_1=(-10)/(2)`

`m_1=-5`

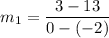
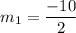
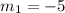
CD formed by (-5,0) and (10,3). So, slope of CD is:

`m_2=(3-0)/(10-(-5))`

`m_2=(3)/(10+5)`

`m_2=(3)/(15)`

`m_2=(1)/(5)`

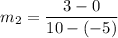
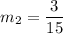
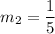
Since
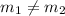`m_1\\eq m_2`, therefore the segments AB and CD are not parallel.

`m_1* m_2=-5* (1)/(5)`

`m_1* m_2=-1`

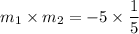
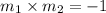
Since
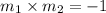`m_1* m_2=-1`, therefore the segments AB and CD are perpendicular because product of slopes of two perpendicular lines is always -1.

Hence, the segments AB and CD are perpendicular.

Answer 2

AB is perpendicular to CD.

Explanation:

AB formed by (-2, 13) and (0, 3)

CD formed by (-5, 0) and (10, 3)

Slope of a line passing through two points is

`m= (y''-y')/(x''- x')`

The slope of line AB is

`m= (3- 13)/(0+2) = -5`

The slope of line CD is

`m'= (3 -0 )/(10+5) = (1)/(5)`

As the product of m and m' is -1 so the lines AB and CD are perpendicular to each other.