Question

A 0.033-kg bullet is fired vertically at 222 m/s into a 0.15-kg baseball that is initially at rest. How high does the combined bullet and baseball rise after the collision, assuming the bullet embeds itself in the ball

Answer 1

The maximum height risen by the bullet-baseball system after the collision is 81.76 m.

Step-by-step explanation:

Given;

mass of the bullet, m₁ = 0.033 kg

mass of the baseball, m₂ = 0.15 kg

initial velocity of the bullet, u₁ = 222 m/s

initial velocity of the baseball, u₂ = 0

let the common final velocity of the system after collision = v

Apply the principle of conservation of linear momentum to determine the common final velocity.

m₁u₁ + m₂u₂ = v(m₁ + m₂)

0.033 x 222 + 0.15 x 0 = v(0.033 + 0.15)

7.326 = v(0.183)

v = 7.326 / 0.183

v = 40.03 m/s

Let the height risen by the system after collision = h

Initial velocity of the system after collision = Vi = 40.03 m/s

At maximum height, the final velocity, Vf = 0

acceleration due to gravity for upward motion, g = -9.8 m/s²

`v_f^2 = v_i^2 +2gh\\\\0 = 40.03^2 - (2* 9.8)h\\\\19.6h = 1602.4\\\\h = (1602.4)/(19.6) \\\\h = 81.76 \ m`

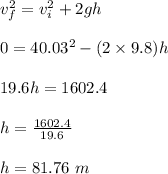
Therefore, the maximum height risen by the bullet-baseball system after the collision is 81.76 m.