Question

SCALCET8 3.9.004.MI. The length of a rectangle is increasing at a rate of 7 cm/s and its width is increasing at a rate of 8 cm/s. When the length is 15 cm and the width is 7 cm, how fast is the area of the rectangle increasing

Answer 1

The area of the rectangle is increasing at a rate of 169 cm²/s

Explanation:

Given;

increase in the length of the rectangle,
`(dL)/(dt) = 7 \ cm/s`

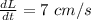
increase in the width of the rectangle,
`(dW)/(dt) = 8 \ cm/s`

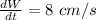
length, L = 15 cm

width, W = 7 cm

The increase in Area is calculated as;

`Area = Length * Width\\\\A = LW\\\\(dA)/(dt) = L((dW)/(dt) )\ + \ W((dL)/(dt) )\\\\(dA)/(dt) = 15 \ cm(8\ ( cm)/(s) ) \ + \ 7 \ cm(7\ ( cm)/(s) ) \\\\(dA)/(dt) = 120 \ cm^2/s \ + \ 49 \ cm^2/s\\\\(dA)/(dt) = 169 \ cm^2/s`

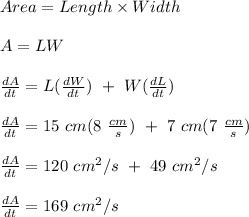
Therefore, the area of the rectangle is increasing at a rate of 169 cm²/s