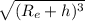Answer:
T = 5.45 10⁻¹⁰
Step-by-step explanation:
Let's use Newton's second law
F = ma
force is the universal force of attraction and acceleration is centripetal
G m M / r² = m v² / r
G M / r = v²
as the orbit is circular, the speed of the satellite is constant, so we can use the kinematic relations of uniform motion
v = d / T
the length of a circle is
d = 2π r
we substitute
G M / r = 4π² r² / T²
T² =
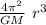
the distance r is measured from the center of the Earth (Re), therefore
r = Re + h
where h is the height from the planet's surface
let's calculate
T² =
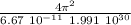 (Re + h) ³
(Re + h) ³
T =
![\sqrt{29.72779 \ 10^(-20)} \ \sqrt[2]{R_e+h)^3}](https://img.qammunity.org/2022/formulas/physics/college/1nbfapuz577d0hm73o2dhxl5vur6vtfiug.png)
T = 5.45 10⁻¹⁰