Question

LMNP is a parallelogram.

On a coordinate plane, parallelogram L M N P is shown. Point L is at (negative 4, 1), point M is at (2, 4), point N is at (3, 2), and point P is at (negative 3, negative 1).

What additional information would prove that LMNP is a rectangle?

The length of LM is StartRoot 45 EndRoot and the length of MN is StartRoot 5 EndRoot.
The slope of LP and MN is –2.
LM ∥ PN
LP ⊥ PN

Answer 1

d

Explanation:

Answer 2

LP ⊥ PN

Explanation:

Given

`L = (-4, 1)`

`M = (2, 4)`

`N = (3, 2)`

`P = (-3, -1)`

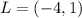
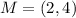
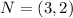
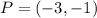
See attachment

Required

What proves LMNP is a rectangle

The additional information needed is LP ⊥ PN

Because:

`(a)\ LM= √(45); MN = √(5)`

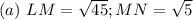
This can be true for other shapes, such as trapezoid, etc.

`(b)\ m(LP) = m(MN) = -2`

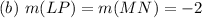
The slopes of LP and MN will be the same because both sides are parallel; However, this is not peculiar to rectangles alone. Same as option (c)

(d) LP ⊥ PN

This must be true i.e. LP must be perpendicular to PN