Answer:
0.0207 = 2.07% approximate probability of finding at least 157 defects
Explanation:
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
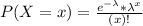
In which
x is the number of sucesses
e = 2.71828 is the Euler number
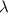 is the mean in the given interval.
is the mean in the given interval.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
n instances of a Poisson distribution can be approximated to a normal distribution, with
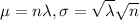
The average defect rate on a 2010 Volkswagen vehicle was reported to be 1.33 defects per vehicle.
This means that
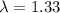
Suppose that we inspect 100 Volkswagen vehicles at random.
This means that
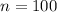
Mean and standard deviation:
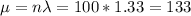
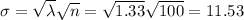
What is the approximate probability of finding at least 157 defects?
Using continuity correction(Poisson is a discrete distribution, normal continuous), this is
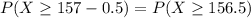 , which is 1 subtracted by the p-value of Z when X = 156.5. So
, which is 1 subtracted by the p-value of Z when X = 156.5. So

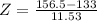
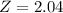
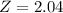 has a p-value of 0.9793.
has a p-value of 0.9793.
1 - 0.9793 = 0.0207
0.0207 = 2.07% approximate probability of finding at least 157 defects