Question

Express the function as the sum of a power series by first using partial fractions. f(x)=x+62x2−9x−5

Answer 1

`(x+6)/(2x^2-9x+5)=-\sum_(n=0)^(\infty) [(-2)^(n)x^(n) + (x^(n))/(5^(n+1))]`

when:

`|x|<(1)/(2)`

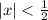
Explanation:

In order to solve this problem, we must begin by splitting the function into its partial fractions, so we must first factor the denominator.

`(x+6)/(2x^2-9x+5)=(x+6)/((2x+1)(x-5))`

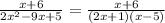
Next, we can build our partial fractions, like this:

`(x+6)/((2x+1)(x-5))=(A)/(2x+1)+(B)/(x-5)`

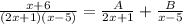
we can then add the two fraction on the right to get:

`(x+6)/((2x+1)(x-5))=(A(x-5)+B(2x+1))/((2x+1)(x-5))`

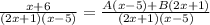
Since we need this equation to be equivalent, we can get rid of the denominators and set the numerators equal to each other, so we get:

`x+6=A(x-5)+B(2x+1)`

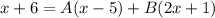
and expand:

`x+6=Ax-5A+2Bx+B`

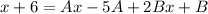
we can now group the terms so we get:

`x+6=Ax+2Bx-5A+B`

`x+6=(Ax+2Bx)+(-5A+B)`

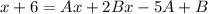
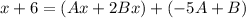
and factor:

`x+6=(A+2B)x+(-5A+B)`

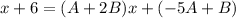
so we can now build a system of equations:

A+2B=1

-5A+B=6

and solve simultaneously, this one can be solved by substitution, so we get>

A=1-2B

-5(1-2B)+B=6

-5+10B+B=6

11B=11

B=1

A=1-2(1)

A=-1

So we can use these values to build our partial fractions:

`(x+6)/((2x+1)(x-5))=(A)/(2x+1)+(B)/(x-5)`

`(x+6)/((2x+1)(x-5))=-(1)/(2x+1)+(1)/(x-5)`

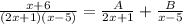
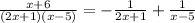
and we can now use the partial fractions to build our series. Let's start with the first fraction:

`-(1)/(2x+1)`

We can rewrite this fraction as:

`-(1)/(1-(-2x))`

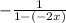
We can now use the following rule to build our power fraction:

`\sum_(n=0)^(\infty) ar^(n) = (a)/(1-r)`

when |r|<1

in this case a=1 and r=-2x so:

`-(1)/(1-(-2x))=-\sum_(n=0)^(\infty) (-2x)^n`

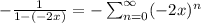
or

`-(1)/(1-(-2x))=-\sum_(n=0)^(\infty) (-2)^(n) x^(n)`

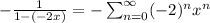
for: |-2x|<1

or:
`|x|<(1)/(2)`

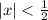
Next, we can work with the second fraction:

`(1)/(x-5)`

On which we can factor a -5 out so we get:

`-(1)/(5(1-(x)/(5)))`

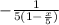
In this case: a=-1/5 and r=x/5

so our series will look like this:

`-(1)/(5(1-(x)/(5)))=-(1)/(5)\sum_(n=0)^(\infty) ((x)/(5))^n`

Which can be simplified to:

`-(1)/(5(1-(x)/(5)))=-\sum_(n=0)^(\infty) (x^n)/(5^(n+1))`

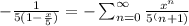
when:

`|(x)/(5)|<1`

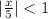
or

|x|<5

So we can now put all the series together to get:

`(x+6)/(2x^2-9x+5)=-\sum_(n=0)^(\infty) [(-2)^(n)x^(n) + (x^(n))/(5^(n+1))}`

when:

`|x|<(1)/(2)`

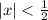
We use the smallest interval of convergence for x since that's the one the whole series will be defined for.