Question

A softball pitcher has a 0.507 probability of throwing a strike for each pitch. If the softball pitcher throws 15 pitches, what is the probability that exactly 8 of them are strikes? Insert the correct symbol to represent this probability.

Answer 1

The probability that the pitcher throws exactly 8 strikes out of 15 pitches is approximately 0.199

Explanation:

The given probability that the pitcher throws a strike, p = 0.507

The number of pitches thrown by the pitcher = 15 pitches

The probability that the pitcher does not throw a strike, q = 1 - P

∴ q = 1 - 0.507 = 0.493

By binomial theorem, we have;

`P(X = r) = \dbinom{n}{r}p^(r) \cdot q^(n-r)= \dbinom{n}{r}p^(r) \cdot \left (1-p \right )^(n-r)`

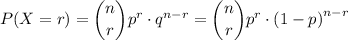
When X = r = 8, and n = 15, we get;

The probability that the pitcher throws exactly 8 strikes out of 15 pitches, P(8), is given as follows

P(8) = ₁₅C₈ × 0.507⁸ × (1 - 0.507)⁽¹⁵ ⁻ ⁸⁾ = 6,435 × 0.507⁸ × 0.493⁷ ≈ 0.199