Answer:
B
Explanation:
Let divide g(x) by f(x)
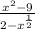
The domain of a rational function cannot equal zero so let set the bottom function to zero.
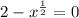
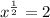
Square both sides
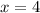
Also we can simplify the bottom denomiator into a square root function
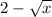
The domain of a square root function is all real number greater than or equal to zero because a square root of a negative number isn't graphable.
So we must find a answer that
- Disincludes 4 from the interval
- Doesnt range in the negative number or infinity)
- Range out in positve infinity
- The answer to that is B