Question

Determine whether the given functions are linearly dependent or linearly independent on the specified interval. Justify your decision.

Answer 1

The question is incomplete. The complete question is :

Determine whether the given functions are linearly dependent or linearly independent on the specified interval. Justify your decision.

`$\{ x^5, x^5-1,3 \} \text{ on } (- \infty, \infty)$`

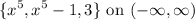
Solution :

Given :

Function :
`$\{ x^5, x^5-1,3 \} \text{ on } (- \infty, \infty)$`

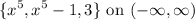
We have to determine whether the given function is linear dependent or linearly independent for the interval
`$(-\infty, \infty)$`.

The given function are linearly dependent because for the constants,
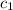`c_1` and
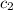`c_2`, the equation is :

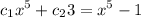`$c_1x^5 + c_23 = x^5-1$` has the solution
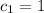`$c_1 = 1$` and
`$c_2 = -(1)/(3)$`

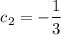
Therefore,

`$1x^5 + \left(-(1)/(3)\right)3 = x^5-1$`