Answer:
The table representing Relationship B is option 2

Explanation:
The relationship shown by Relationship A and Relationship B = The change in the temperature for a pot of water om the stove
The rate of Relationship B > The rate of Relationship A
The table for relationship A is given as follows';
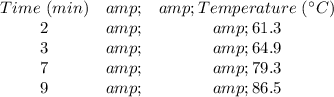
The time in minutes are the x-values, while the temperature in °C Ere the y-values
The rate for Relationship A,
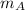 = (86.5 - 61.3)/(9 - 2) = 3.6
= (86.5 - 61.3)/(9 - 2) = 3.6
Therefore, the rate for Relationship B > 3.6
By checking each option, we note that in option 2, the maximum value for the y-value is the same as for Relationship A, which is 86.5°C, while the minimum value for the time, t, is lesser than that for Relationship A, (60.6 minutes < 61.3 minutes) therefore, we get;
The rate for option 2 = (86.5 - 60.6)/(9 - 2) = 3.7
Therefore, the table that represents the Relationship B is the table for option 2
