Answer:
Here we just want to find the Taylor series for f(x) = ln(x), centered at the value of a (which we do not know).
Remember that the general Taylor expansion is:
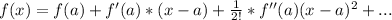
for our function we have:
f'(x) = 1/x
f''(x) = -1/x^2
f'''(x) = (1/2)*(1/x^3)
this is enough, now just let's write the series:
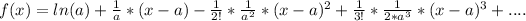
This is the Taylor series to 3rd degree, you just need to change the value of a for the required value.