Answer:
A point on the edge of the wheel will travel 199.563 radians at the given time.
Step-by-step explanation:
Given;
initial angular velocity of the wheel;
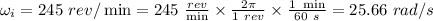
final angular velocity of the wheel;
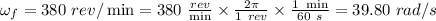
radius of the wheel, d/2 = (30 cm ) / 2 = 15 cm = 0.15 m
time of motion, t = 6.1 s
The angular distance traveled by the edge of the wheel is calculated as;
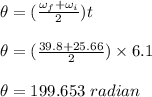
Therefore, a point on the edge of the wheel will travel 199.563 radians at the given time.