Answer:
The probability of observing between 43 and 64 successes=0.93132
Explanation:
We are given that
n=100
p=0.50
We have to find the probability of observing between 43 and 64 successes.
Let X be the random variable which represent the success of population.
It follows binomial distribution .
Therefore,
Mean,
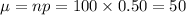
Standard deviation ,

![\sigma=\sqrt{100* 0.50(1-0.50)]](https://img.qammunity.org/2022/formulas/mathematics/college/llmwfu63a8nwtn8yai18ftpikyc754vwu5.png)
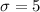
Now,

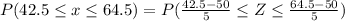
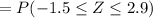
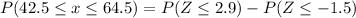
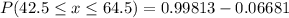

Hence, the probability of observing between 43 and 64 successes=0.93132