Solution :
The objective is to obtain the
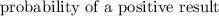 for 2 samples combined into a
for 2 samples combined into a
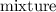 .
.
Given that the

The probability of the positive test result is calculated as follows :
P ( positive mixture ) = P(1 or more samples positive)
= 1 - P (none +ve)
= 1 - P ((-ve) x (-ve))
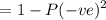
![$=1-[1-P(+ve)]^2$](https://img.qammunity.org/2022/formulas/mathematics/college/g3f5y6w706houf5dqolwfegn258i9utx0q.png)
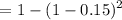
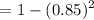
= 1 - 0.7225
= 0.2775
No, the probability is not low enough.