Answer:
The answer is
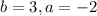 , and
, and
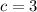 .
.
Explanation:
To solve this system of equations, start by solving for (a) in the third equation.
To solve for (a) in the third equation, add
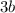 to both sides of the equation, which will look like
to both sides of the equation, which will look like
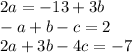 . Next, divide each term in
. Next, divide each term in
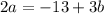 by 2 and simplify, which will look like
by 2 and simplify, which will look like
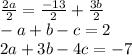 =
=
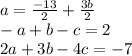 .
.
Then, replace all variables of (a) with
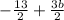 in each equation and simplify, which will look like
in each equation and simplify, which will look like
 .
.
The next step is to reorder
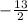 and
and
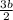 , which will look like
, which will look like
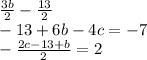 .
.
Then, solve for (b) in the second equation. To solve for (b) in the second equation start by moving all terms not containing (b) to the right side of the equation, which will look like
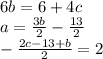 . Next, divide each term in (
. Next, divide each term in (
 ) and simplify, which will look like
) and simplify, which will look like
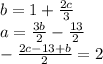 .
.
Then, replace all variables of (b) with
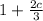 in each equation and simplify, which will look like
in each equation and simplify, which will look like
 .
.
The next step is to solve for (c) in the first equation. To solve for (c) in the first equation start by multiplying both sides of the equation by
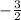 and simplify, which will look like
and simplify, which will look like
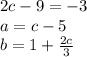 . Then, move all terms not containing (c) to the right side of the equation, which will look like
. Then, move all terms not containing (c) to the right side of the equation, which will look like
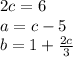 . Next, divide each term in
. Next, divide each term in
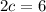 by 2 and simplify, which will look like
by 2 and simplify, which will look like
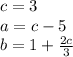 .
.
Then, replace all variables of (c) with 3 in each equation and simplify, which will look like
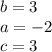 . Finally, the list of all the solutions are
. Finally, the list of all the solutions are
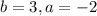 , and
, and
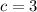 .
.