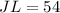Question

If K is the midpoint of JL, JK = 8x + 11 and KL = 14x – 1, find JL.​

Answer 1

`JL=54`

Explanation:

We are given that K is the midpoint of JL. Using this information, we want to find JL.

By the definition of midpoint, this means that:

`JK=KL`

Substitute them for their equations:

`8x+11=14x-1`

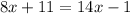
Solve for x. Subtract 8x from both sides:

`11=6x-1`

Add 1 to both sides:

`6x=12`

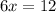
And divide both sides by 6. Hence:

`x=2`

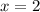
JL is the sum of JK and KL. Hence:

`JK+KL=JL`

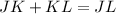
Since JK = KL, substitute either one for the other:

`JK+(JK)=2JK=JL`

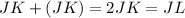
Substitute JK for its equation:

`2(8x+11)=JL`

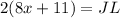
Since we know that x = 2:

`2(8(2)+11)=2(16+11)=2(27)=54=JL`

Thus:

`JL=54`