Question

We are throwing darts on a disk-shaped board of radius 5. We assume that the proposition of the dart is a uniformly chosen point in the disk. The board has a disk-shaped bullseye with radius 1. Suppose that we throw a dart 2000 times at the board. Estimate the probability that we hit the bullseye at least 100 times.

Answer 1

the probability that we hit the bullseye at least 100 times is 0.0113

Explanation:

Given the data in the question;

Binomial distribution

We find the probability of hitting the dart on the disk

⇒ Area of small disk / Area of bigger disk

⇒ πR₁² / πR₂²

given that; disk-shaped board of radius R² = 5, disk-shaped bullseye with radius R₁ = 1

so we substitute

⇒ π(1)² / π(5)² = π/π25 = 1/25 = 0.04

Since we have to hit the disk 2000 times, we represent the number of times the smaller disk ( BULLSEYE ) will be hit by X.

so

X ~ Bin( 2000, 0.04 )

n = 2000

p = 0.04

np = 2000 × 0.04 = 80

Using central limit theorem;

X ~ N( np, np( 1 - p ) )

we substitute

X ~ N( 80, 80( 1 - 0.04 ) )

X ~ N( 80, 80( 0.96 ) )

X ~ N( 80, 76.8 )

So, the probability that we hit the bullseye at least 100 times, P( X ≥ 100 ) will be;

we covert to standard normal variable

⇒ P( X ≥
`(100-80)/(√(76.8) )` )

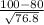⇒ P( X ≥ 2.28217 )

From standard normal distribution table

P( X ≥ 2.28217 ) = 0.0113

Therefore, the probability that we hit the bullseye at least 100 times is 0.0113