Answer: Choice C)
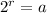
This is the same as writing 2^r = a
==========================================================
Step-by-step explanation:
Assuming that '2' is the base of the log, then we'd go from
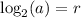 to
to
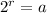
In either equation, the 2 is a base of some kind. It's the base of the log and it's the base of the exponent.
The purpose of logs is to invert exponential operations and help isolate the exponent. A useful phrase to help remember this may be: "if the exponent is in the trees, then we need to log it down".
The general rule is that
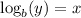 converts to
converts to
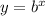 and vice versa.
and vice versa.