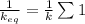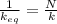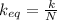Question

now suppose that we have attached not just two springs in series, but N springs. Write an equation that expresses the effective spring constant of the combination using the spring constant of the original spring k and the number of springs N

Answer 1

`k_(eq) = (k)/(N)`

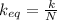
Step-by-step explanation:

For this exercise let's use hooke's law

F = - k x

where x is the displacement from the equilibrium position.

x =
`- (F)/(k)`

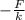
if we have several springs in series, the total displacement is the sum of the displacement for each spring, F the external force applied to the springs

x_ {total} = ∑ x_i

we substitute

x_ {total} = ∑ -F / ki

F / k_ {eq} = -F
`\sum (1)/(k_i)`

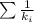
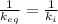`(1)/(k_(eq)) = (1)/(k_i)` 1 / k_ {eq} = ∑ 1 / k_i

if all the springs are the same

k_i = k

`(1)/(k_(eq)) = (1)/(k) \sum 1 \\`

`(1)/(k_(eq) ) = (N)/(k)`

`k_(eq) = (k)/(N)`