Answer:
The rate at which the distance between the cars increasing two hours later=52mi/h
Explanation:
Let
Speed of one car, x'=48 mi/h
Speed of other car, y'=20 mi/h
We have to find the rate at which the distance between the cars increasing two hours later.
After 2 hours,
Distance traveled by one car
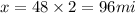
Using the formula
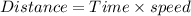
Distance traveled by other car
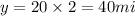
Let z be the distance between two cars after 2 hours later
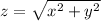
Substitute the values
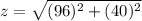
z=104 mi
Now,
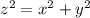
Differentiate w.r.t t
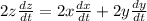
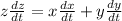
Substitute the values
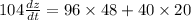
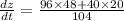
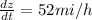
Hence, the rate at which the distance between the cars increasing two hours later=52mi/h