Answer:
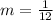
Explanation:
Given
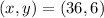
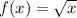 ----- the equation of the curve
----- the equation of the curve
Required
The slope of f(x)
The slope (m) is calculated using:
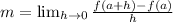
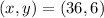 implies that:
implies that:
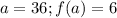
So, we have:
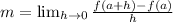
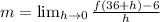
If
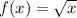 ; then:
; then:
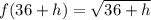
So, we have:
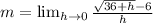
Multiply by:
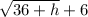
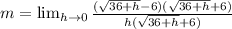
Expand the numerator
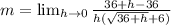
Collect like terms
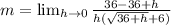
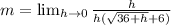
Cancel out h

 implies that we substitute 0 for h;
implies that we substitute 0 for h;
So, we have:
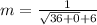
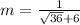
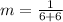
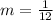
Hence, the slope is 1/12