Answer:
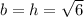 m
m
Explanation:
Let
Bas length of box=b
Height of box=h
Material used in constructing of box=36 square m
We have to find the height h and base length b of the box to maximize the volume of box.
Surface area of box=

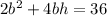
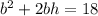
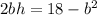
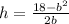
Volume of box, V=
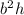
Substitute the values
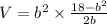
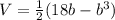
Differentiate w. r.t b
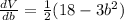
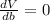
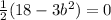
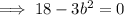
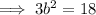
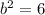
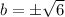
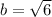
The negative value of b is not possible because length cannot be negative.
Again differentiate w.r.t b
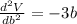
At
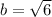
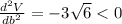
Hence, the volume of box is maximum at
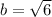 .
.
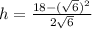
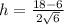
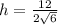
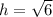
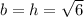 m
m