Answer:
It will take about 109.3 seconds for nine grams of the element to decay to 0.72 grams.
Explanation:
We can write a half-life function to model our function.
A half-life function has the form:
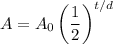
Where A₀ is the initial amount, t is the time that has passes (in this case seconds), d is the half-life, and A is the amount after t seconds.
Since the half-life of the element is 30 seconds, d = 30. Our initial sample has nine grams, so A₀ is 9. Substitute:
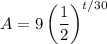
We want to find the time it will take for the element to decay to 0.72 grams. So, we can let A = 0.72 and solve for t:
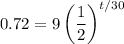
Divide both sides by 9:
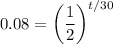
We can take the natural log of both sides:
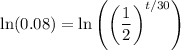
By logarithm properties:
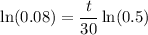
Solve for t:
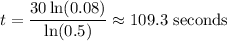
So, it will take about 109.3 seconds for nine grams of the element to decay to 0.72 grams.