Question

The half-life of a newly discovered radioactive element is 30 seconds. To the nearest tenth of a second, how long will it take for a sample of 9 grams to decay to 0.72 grams

Answer 1

It will take about 109.3 seconds for nine grams of the element to decay to 0.72 grams.

Explanation:

We can write a half-life function to model our function.

A half-life function has the form:

`\displaystyle A=A_0\left((1)/(2)\right)^(t/d)`

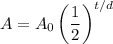
Where A₀ is the initial amount, t is the time that has passes (in this case seconds), d is the half-life, and A is the amount after t seconds.

Since the half-life of the element is 30 seconds, d = 30. Our initial sample has nine grams, so A₀ is 9. Substitute:

`\displaystyle A=9\left((1)/(2)\right)^(t/30)`

We want to find the time it will take for the element to decay to 0.72 grams. So, we can let A = 0.72 and solve for t:

`\displaystyle 0.72=9\left((1)/(2)\right)^(t/30)`

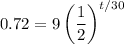
Divide both sides by 9:

`\displaystyle 0.08=\left((1)/(2)\right)^(t/30)`

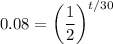
We can take the natural log of both sides:

`\displaystyle \ln(0.08)=\ln\left(\left((1)/(2)\right)^(t/30)\right)`

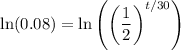
By logarithm properties:

`\displaystyle \ln(0.08)=(t)/(30)\ln(0.5)`

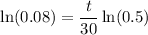
Solve for t:

`\displaystyle t=(30\ln(0.08))/(\ln(0.5))\approx109.3\text{ seconds}`

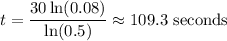
So, it will take about 109.3 seconds for nine grams of the element to decay to 0.72 grams.