Question

A tire is filled with air at 22oC to a gauge pressure of 240 kPa. After driving for some time, if the temperature of air inside the tire is 45oC, what fraction of the original volume of air must be removed to maintain the pressure at 240 kPa?

Answer 1

7.8% of the original volume.

Step-by-step explanation:

From the given information:

Temperature
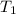`T_1` = 22° C = 273 + 22 = 295° C

Pressure
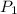`P_1` = 240 kPa

Temperature
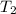`T_2` = 45° C

At initial temperature and pressure:

Using the ideal gas equation:

`P_1V_1 =nRT_1`

making V_1 (initial volume) the subject:

`V_1 = (nRT_1)/(P_1)`

`V_1 = (nR*295)/(240)`

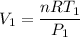
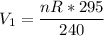
Provided the pressure maintained its rate at 240 kPa, when the temperature reached 45° C, then:

the final volume
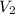`V_2` can be computed as:

`V_2 = (nR*318)/(240)`

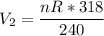
Now, the change in the volume ΔV = V₂ - V₁

`\Delta V = (nR*318)/(240)- (nR*295)/(240)`

`\Delta V = (23nR)/(240)`

∴

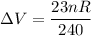
The required fraction of the volume of air to keep up the pressure at (240) kPa can be computed as:

`= ((23nR)/(240))/( (295nR)/(240))`

`= {(23nR)/(240)} * { (240)/(295nR)}`

`= 0.078`

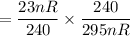
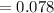
= 7.8% of the original volume.