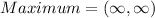Answer:
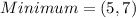
No maximum
Explanation:
Given

Solving (a): The minimum
The minimum is when the absolute parameter gives 0
i.e.
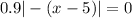
Divide both sides by 0.9
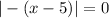
Open bracket
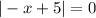
Remove absolute sign
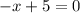
Collect like terms
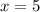
Then the y value is:

Recall that:
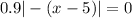
So, we have:
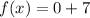
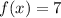
Hence, the minimum is at:

Since the minimum is at
 , then the graph will open upwards.
, then the graph will open upwards.
Hence. the function has no maximum; i.e.