Answer:
The values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.001 is 0 < x < 0.3936.
Explanation:
Note: This question is not complete. The complete question is therefore provided before answering the question as follows:
Determine the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.001. f(x) = e^x ≈ 1 + x + x²/2! + x³/3!, x < 0
The explanation of the answer is now provided as follows:
Given:
f(x) = e^x ≈ 1 + x + x²/2! + x³/3!, x < 0 …………….. (1)
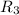 = (x) = (e^z /4!)x^4
= (x) = (e^z /4!)x^4
Since the aim is
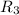 (x) < 0.001, this implies that:
(x) < 0.001, this implies that:
(e^z /4!)x^4 < 0.0001 ………………………………….. (2)
Multiply both sided of equation (2) by (1), we have:
e^4x^4 < 0.024 ……………………….......……………. (4)
Taking 4th root of both sided of equation (4), we have:
|xe^(z/4) < 0.3936 ……………………..........…………(5)
Dividing both sides of equation (5) by e^(z/4) gives us:
|x| < 0.3936 / e^(z/4) ……………….................…… (6)
In equation (6), when z > 0, e^(z/4) > 1. Therefore, we have:
|x| < 0.3936 -----> 0 < x < 0.3936
Therefore, the values of x for which the function can be replaced by the Taylor polynomial if the error cannot exceed 0.001 is 0 < x < 0.3936.