Answer:
She will need 41.22 meters.
Explanation:
She knows that one leg of the triangle is 11 meters long and that the angle formed by that leg and the hypotenuse is 50 degrees .
The leg is adjacent to the hypothenuse. We know that the cosine of an angle
 is given by:
is given by:
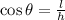
In which l is the length of the adjacent side and h is the hypothenuse.
Considering that we have
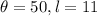 , we can find the hypothenuse.
, we can find the hypothenuse.
Looking at a calculator, the cosine of 50 degrees is 0.6428.
So

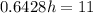
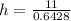

The other leg:
In a right triangle, with legs
 and
and
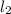 , and hypothenuse h, the pythagorean theorem states that:
, and hypothenuse h, the pythagorean theorem states that:
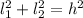
We already have one of the legs and the hypothenuse, so:
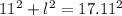

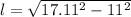
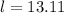
How many meters will she need?
This is the perimeter of the garden, which is the sum of its dimensions, of 11 meters, 13.11 meters and 17.11 meters. So
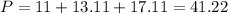
She will need 41.22 meters.