Answer:

The mean of the distribution is 0.25.
The variance of the distribution is of 0.6875.
Explanation:
Probability density function:
For it to be a probability function, the sum of the probabilities must be 1. The probabilities are 3c, 3c and 6c, so:
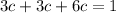
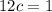

So the probability distribution is:
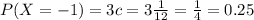
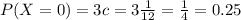
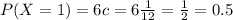
Mean:
Sum of each outcome multiplied by its probability. So
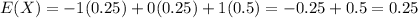
The mean of the distribution is 0.25.
Variance:
Sum of the difference squared between each value and the mean, multiplied by its probability. So
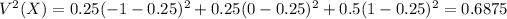
The variance of the distribution is of 0.6875.