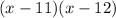Answer:
(x-11)(x-12)
Explanation:
To clarify, there was a likely typo written in your question since it is impossible to solve two unknown values with only one equation. I'm supposing that the equation was supposed to be
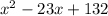
The first step is to split the term into factorable terms.
Since the highest power is power of 2, the equation would look like this if factorized:
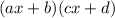
If the terms were added properly, the expanded equation would be:
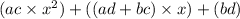
Generally, we do not see decimal values or fractions in factorization with some exceptions. Otherwise, the equation could get very complicated.
In this case, we can determine the following:
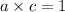
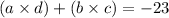
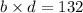
First, we can determine a and c to be one since one only has one factor, which is itself.
This leaves us with two equations left
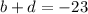
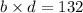
There are two ways to solve the remaining two terms. We can either find the factors or do quadratic equation. Finding the factors is the easier way out here.
b and d will add up to negative values but multiplying these values give positive values. The most likely reason is that b and d are negative values.
Now, we can find the factors of 132.
The factors are 1, 2, 3, 4 , 6, 11, 12, 22, 33, 44, 66 and 132. However, the values flip around.
In fact, the "factors" we are looking for are the negative values of the actual factors. To solve this, we should find two factors that add up to 23.
In this case, 11+12=23.
To verify, 11*12 is also 132.
Since we are looking for the negative values, the values we are looking for are -11 and -12.
The values can be plugged in anywhere in b or d.
After cleaning up, we can plug in the values into our factorization and we will get:
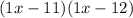
or