Question

~~~NEED HELP ASAP~~~
Please solve each section and show all work for each section.

Answer 1

Step-by-step explanation:

Forces on Block A:

Let the x-axis be (+) towards the right and y-axis be (+) in the upward direction. We can write the net forces on mass
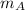`m_A` as

`x:\:\:(F_(net))_x = f_N - T = -m_Aa\:\:\:\:\:\:\:(1)`

`y:\:\:(F_(net))_y = N - m_Ag = 0 \:\:\:\:\:\:\:\:\:(2)`

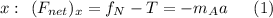
Substituting (2) into (1), we get

`\mu_km_Ag - T = -m_Aa \:\:\:\:\:\:\:\:\:(3)`

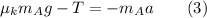
where
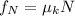`f_N= \mu_kN`, the frictional force on
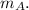`m_A.` Set this aside for now and let's look at the forces on
`m_B`

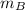
Forces on Block B:

Let the x-axis be (+) up along the inclined plane. We can write the forces on
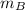`m_B` as

`x:\:\:(F_(net))_x = T - m_B\sin30= -m_Ba\:\:\:\:\:\:\:(4)`

`y:\:\:(F_(net))_y = N - m_Bg\cos30 = 0 \:\:\:\:\:\:\:\:\:(5)`

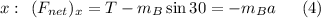
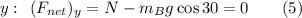
From (5), we can solve for N as

`N = m_B\cos30 \:\:\:\:\:\:\:\:\:(6)`

Set (6) aside for now. We will use this expression later. From (3), we can see that the tension T is given by

`T = m_A( \mu_kg + a)\:\:\:\:\:\:\:\:\:(7)`

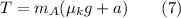
Substituting (7) into (4) we get

`m_A(\mu_kg + a) - m_Bg\sin 30 = -m_Ba`

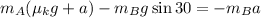
Collecting similar terms together, we get

`(m_A + m_B)a = m_Bg\sin30 - \mu_km_Ag`

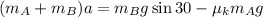
or

`a = \left[ (m_B\sin30 - \mu_km_A)/((m_A + m_B)) \right]g\:\:\:\:\:\:\:\:\:(8)`

Putting in the numbers, we find that
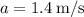`a = 1.4\:\text{m/s}`. To find the tension T, put the value for the acceleration into (7) and we'll get
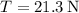`T = 21.3\:\text{N}`. To find the force exerted by the inclined plane on block B, put the numbers into (6) and you'll get
`N = 50.9\:\text{N}`