Answer:
The confidence interval is
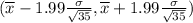 , in which
, in which
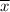 is the sample mean and
is the sample mean and
 is the standard deviation for the population.
is the standard deviation for the population.
Explanation:
We have that to find our
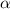 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
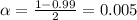
Now, we have to find z in the Z-table as such z has a p-value of
 .
.
That is z with a pvalue of
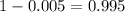 , so Z = 2.575.
, so Z = 2.575.
Now, find the margin of error M as such
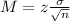
In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
In this question:
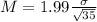
The lower end of the interval is the sample mean subtracted by M, while upper end of the interval is the sample mean added to M. Thus, the confidence interval is
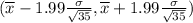 , in which
, in which
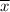 is the sample mean and
is the sample mean and
 is the standard deviation for the population.
is the standard deviation for the population.