Answer:
0.4444 = 44.44% probability that the sum of the two numbers is greater than 3 but less than 7.
Explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
A number is selected at random from each of the sets {2,3,4} and {1, 3, 5}.
The possible values for the sum are:
2 + 1 = 3
2 + 3 = 5
2 + 5 = 7
3 + 1 = 4
3 + 3 = 6
3 + 5 = 8
4 + 1 = 5
4 + 3 = 7
4 + 5 = 9
Find the probability that the sum of the two numbers is greater than 3 but less than 7?
4 of the 9 sums are greater than 3 but less than 7. So
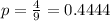
0.4444 = 44.44% probability that the sum of the two numbers is greater than 3 but less than 7.