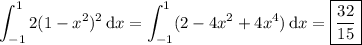Question

Find the volume of the solid lying between two planes perpendicular to the x-axis at x = −1 and x = 1. The cross sections perpendicular to the x-axis are squares whose diagonals run from y = x 2 to y = 2 − x 2

Answer 1

I've attached a sketch of one such cross section (light blue) of the solid (shown at x = 0). The planes x = ±1 are shown in gray, and the two parabolas are respectively represented by the blue and orange curves in the (x, y)-plane.

For every x in the interval [-1, 1], the corresponding cross section has a diagonal of length (2 - x ²) - x ² = 2 (1 - x ²). The diagonal of any square occurs in a ratio to its side length of √2 : 1, so the cross section has a side length of 2/√2 (1 - x ²) = √2 (1 - x ²), and hence an area of (√2 (1 - x ²))² = 2 (1 - x ²)².

The total volume of the solid is then given by the integral,

`\displaystyle\int_(-1)^1 2(1-x^2)^2\,\mathrm dx = \int_(-1)^1 (2-4x^2+4x^4)\,\mathrm dx = \boxed{(32)/(15)}`