Question

Which values are soloutions to the inequality -3x - 4 < 2 ? check all of the boxes that apply

Answer 1

Given:

The inequality is:

`-3x-4<2`

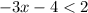
To find:

The values that are solutions to the given inequality.

Solution:

We have,

`-3x-4<2`

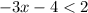
Adding 4 on both sides, we get

`-3x-4+4<2+4`

`-3x<6`

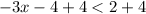
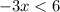
Divide both sides by -3 and change the inequality sign because -3 is a negative value.

`(-3x)/(-3)>(6)/(-3)`

`x>-2`

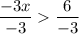
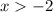
Therefore, all the real values greater than -2 are the solutions to the given inequality.