Question

Unknown mean μ

yielded x¯
x
¯
= 123 and s = 28. Assume σ
σ
= 25. Construct a 90% confidence interval for

Answer 1

The answer is below

Step-by-step explanation:

The question is not complete, but I will solve a similar question. The question goes as:

A random sample of n measurements was selected from a population with unknown mean µ and known standard deviation σ. Calculate a 90% confidence interval for n = 49, ¯ x = 28, σ = 28

Solution:

A confidence interval is a range of numbers that contains a population parameter.

C = 90% = 0.9

α = 1 - C = 1 - 0.9 = 0.1

α/2 = 0.1/2 = 0.05

The z score of α/2 is the same as the z score 0.45 (0.5 - 0.05) which is equal to 1.65. Hence, the margin of error E is:

`E=z_(\alpha)/(2)*(\sigma)/(√(n) ) =1.65*(28)/(√(49) ) =6.6`

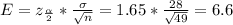
The confidence interval =
`\bar x \pm E=28 \pm 6.6 = (21.4,\ 34.6)`

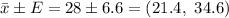
The 90% confidence is between 21.4 and 34.6.