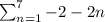Question

Use sigma notation to represent the sum of the first seven terms of the following sequence: −4, −6, −8, …

Answer 1

`\sum_(n = 1)^(7) -2 -2n`

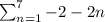
Explanation:

Arithmetic sequence:

In an arithmetic sequence, the difference of consecutive terms is always the same, called common difference.

The nth term of a sequence is given by:

`a_(n) = a_1 + (n-1)d`

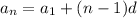
In which
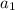`a_1` is the first term and d is the common difference.

Sigma notation to represent the sum of the first seven terms

Sum going from the index starting at 1 and finishing at 7, that is:

`\sum_(n = 1)^(7) f(n)`

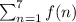
Now we have to fund the function, which is given by an arithmetic sequence.

−4, −6, −8,

First term -4, common difference - 6 - (-4) = -6 + 4 = -2, so
`a_1 = -4, d = -2`

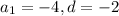
Then

`f(n) = a_(n) = a_1 + (n-1)d`

`f(n) = -4 + (n-1)(-2)`

`f(n) = -4 - 2n + 2 = -2 - 2n`

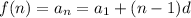
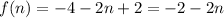
Sigma notation:

Replacing f(n)

`\sum_(n = 1)^(7) -2 -2n`