Answer:
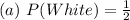
(b) 10 additional white balls
(c) 10 additional black balls
Explanation:
Given
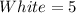
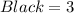

Solving (a): P(White)
This is calculated as:
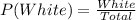

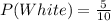

Solving (b): Additional white balls, if
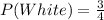
Let the additional white balls be x
So:
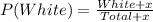
This gives:
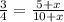
Cross multiply
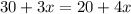
Collect like terms
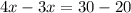
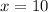
Hence, 10 additional white balls must be added
Solving (c): Additional black balls, if
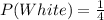
Let the additional black balls be x
So:
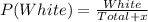
So, we have:
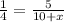
Cross multiply
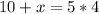

Collect like terms
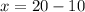
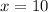
Hence, 10 additional black balls must be added